Algebra 2 Functions Domain And Range
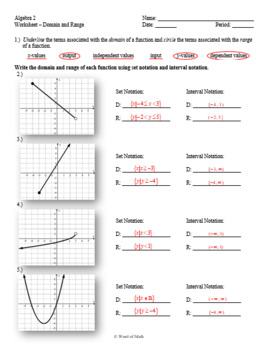
Algebra 2 Domain And Range Of Functions Guided Notes And Worksheet Finding domain and range from graphs. another way to identify the domain and range of functions is by using graphs. because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x axis. the range is the set of possible output values, which are shown on the y axis. keep in mind. The range also excludes negative numbers because the square root of a positive number x is defined to be positive, even though the square of the negative number − √x also gives us x. figure 3.3.20: cube root function f(x) = 3√x. for the cube root function f(x) = 3√x, the domain and range include all real numbers.

Algebra 2 Domain And Range Of Functions Guided Notes And Worksheet The graph goes only as high as the vertex, at y = 4, but it will go as low as i like. so the range is "all y ≤ 4 ". this is the second piece of information they'd wanted, so my hand in answer is: domain: all x. range: y ≤ 4. you can use the mathway widget below to practice finding the domains and ranges of functions. The codomain is actually part of the definition of the function. and the range is the set of values that actually do come out. example: we can define a function f (x)=2x with a domain and codomain of integers (because we say so). but by thinking about it we can see that the range (actual output values) is just the even integers. Example: finding the domain and range using toolkit functions find the domain and range of [latex]f\left(x\right)=2{x}^{3} x[ latex]. answer: there are no restrictions on the domain, as any real number may be cubed and then subtracted from the result. But it is not a function over the domain of real numbers. this graph is undefined when x = 2, because substituting two into the function will create a zero denominator. if we restrict the domain to be "all real numbers excluding 2", our relation can be called a function. domain of the function:.

Algebra 2 Domain And Range Of Functions Guided Notes And Worksheet Example: finding the domain and range using toolkit functions find the domain and range of [latex]f\left(x\right)=2{x}^{3} x[ latex]. answer: there are no restrictions on the domain, as any real number may be cubed and then subtracted from the result. But it is not a function over the domain of real numbers. this graph is undefined when x = 2, because substituting two into the function will create a zero denominator. if we restrict the domain to be "all real numbers excluding 2", our relation can be called a function. domain of the function:. Correct answer: domain: all real numbers. range: explanation: the domain includes the values that go into a function (the x values) and the range are the values that come out (the or y values). a sine curve represent a wave the repeats at a regular frequency. based upon this graph, the maximum is equal to 1, while the minimum is equal to –1. Find the domain and range of the function `f(x)=sqrt(x 2) (x^2 9),` without using a graph. solution. in the numerator (top) of this fraction, we have a square root. to make sure the values under the square root are non negative, we can only choose `x` values grater than or equal to 2.
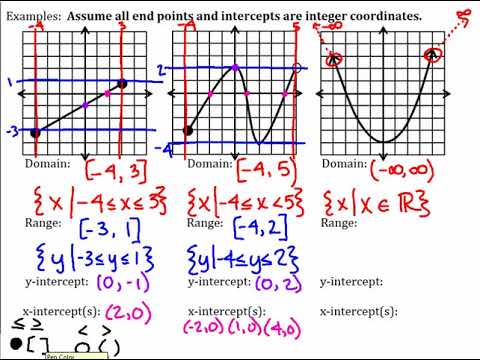
Algebra 2 Unit 1 Day 1 Domain Range End Behavior And Intercepts Youtube Correct answer: domain: all real numbers. range: explanation: the domain includes the values that go into a function (the x values) and the range are the values that come out (the or y values). a sine curve represent a wave the repeats at a regular frequency. based upon this graph, the maximum is equal to 1, while the minimum is equal to –1. Find the domain and range of the function `f(x)=sqrt(x 2) (x^2 9),` without using a graph. solution. in the numerator (top) of this fraction, we have a square root. to make sure the values under the square root are non negative, we can only choose `x` values grater than or equal to 2.

Algebra 2 Unit 5 Day 3 Domain Range And End Behavior Youtube

Comments are closed.