Diagonals Ac And Bd Of Trapezium Abcd With Ab Is Parallel To Dc Intersect Each Other At Point O

By hotyogaworld On Nov 6, 2024 Last updated

Ex 6 3 3 Diagonals Ac And Bd Of A Trapezium Abcd Ex 6 3 Ex 6.3, 3 diagonals ac and bd of a trapezium abcd with ab || dc intersect each other at the point o. using a similarity criterion for two triangles, show that. Class 10 maths ncert solutions chapter 6 exercise 6.3 question 3. summary: for diagonals ac and bd of a trapezium abcd with ab || dc intersecting each other at the.

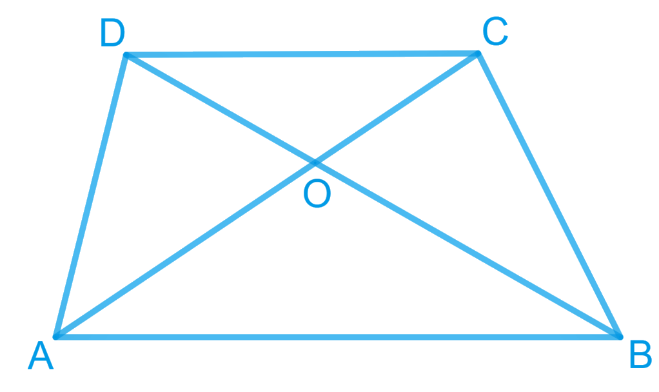
Diagonals Ac And Bd Of A Trapezium Abcd With Ab Dc Intersect Each Other At O Prove That Ar Click here:point up 2:to get an answer to your question :writing hand:diagonals ac and bd of a trapezium abcd with ab3. Abcd is a trapezium in which ab parallel dcand its diagonals intersect each other at point o . show that ao bo= co do. In each of the figures [(i) (iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line segment are marked. find the value of x in each of the following :. The diagonals ac and bd intersect at o. we have to prove using similarity criterion for two triangles that $\dfrac{oa}{oc}=\dfrac{ob}{od}$. let us first draw the trapezium with the given details.

Question 2 Diagonals Of A Trapezium Abcd With Ab Dc In each of the figures [(i) (iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line segment are marked. find the value of x in each of the following :. The diagonals ac and bd intersect at o. we have to prove using similarity criterion for two triangles that $\dfrac{oa}{oc}=\dfrac{ob}{od}$. let us first draw the trapezium with the given details. Hint:in this question, they give the relation in the trapezium.so, here we have to use the similarity criterion for two triangles to prove the requirement result. we know that the corresponding sides of the two triangles are in proportion when the two triangles are similar. ☛ related questions: in fig. 6.22, line segment df intersect the side ac of a triangle abc at the point e such that e is . . . . prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to . . . .

Explore the Wonders of Science and Innovation: Dive into the captivating world of scientific discovery through our Diagonals Ac And Bd Of Trapezium Abcd With Ab Is Parallel To Dc Intersect Each Other At Point O section. Unveil mind-blowing breakthroughs, explore cutting-edge research, and satisfy your curiosity about the mysteries of the universe.

Diagonals AC and BD of trapezium ABCD with AB is parallel to DC intersect each other at point O.

Diagonals AC and BD of trapezium ABCD with AB is parallel to DC intersect each other at point O. Diagonals AC and BD of a trapezium ABCD with AB || DC | Q3 Exercise 6.3 Class 10 diagonals of a trapezium ABCD with AB//DC intersect each other at the point O. If AB=2CD find the .. Diagonals AC and BD of trapezium ABCD with AB||DC intersect each other at point O show.. Diagonals AC and BD of a trapezium ABCD with AB || DC. Show that AO/OC = OB/OD Diagonal AC And BD Of A Trapezium ABCD With AB || DC Intersect Each Other At The Point O Q3,Q4|Diagonals AC , BD of trapezium ABCD with AB||DC intersect at point O & QR/ QT=QS/ PR ,∠1 =∠2. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using... Diagonals of AC and BD of a trapezium ABCD with AB//DC intersect each other at O, using similarity . The diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find... Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using... Diagonalsof a trapezium ABCD with AB || DC intersect each other at the point O. If AB= 2 CD, fin... Diagonals Of A Trapezium ABCD With AB || DC Intersect Each Other At The Point O If AB = 2CD The diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the Diagonals AC and BD of a trapezium ABCD with ABllDC intersect each other at the point O. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point o Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using... Diagonals AC And BD Of a Trapezium ABCD With AB Parallel To DC Intersect Each Other At The Point O Question no.3 || Triangles || Exercise - 6.3 || NCERT || Class 10 Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O.If AB = 2 CD,

Conclusion

Delving deeply into the topic, there is no doubt that piece supplies useful data regarding Diagonals Ac And Bd Of Trapezium Abcd With Ab Is Parallel To Dc Intersect Each Other At Point O. From beginning to end, the commentator depicts substantial skill about the subject matter. Significantly, the examination of this aspect stands out as a major point. On top of that, the write-up shines in disentangling complex concepts in an clear manner. Also, the essayist supplies applicable examples that heighten the understanding. A supplementary feature that makes this piece exceptional is the comprehensive analysis of a range of aspects related to Diagonals Ac And Bd Of Trapezium Abcd With Ab Is Parallel To Dc Intersect Each Other At Point O. The writers scrupulous manner guarantees that observers acquire a full grasp of the subject matter. Thanks for taking the time to this composition. For more details, dont hesitate to send an email leveraging my email address. I am keen on your interactions. In finishing up, for additional information, noted below are a collection of associated posts that might be beneficial:Wishing you a great reading experience!