Las Rectas Perpendiculares Definiciгіn Y Ejemplo
Las Rectas Perpendiculares Definición Y Ejemplo 4 análisis de pendientes en rectas perpendiculares. 5 ejemplos clave de rectas perpendiculares. 5.1 ejemplo 1: rectas en el plano cartesiano. 5.2 ejemplo 2: uso de vectores. 6 aplicaciones en la geometría y el diseño. 7 conclusión. 8 recursos adicionales para profundizar en el tema. Rectas perpendiculares (perpendicularidad) en esta página encontrarás todo sobre las rectas perpendiculares: qué son, cuándo dos rectas son perpendiculares, cómo calcular una recta perpendicular a otra, sus propiedades,…. además, podrás ver ejemplos y podrás practicar con ejercicios resueltos paso a paso.

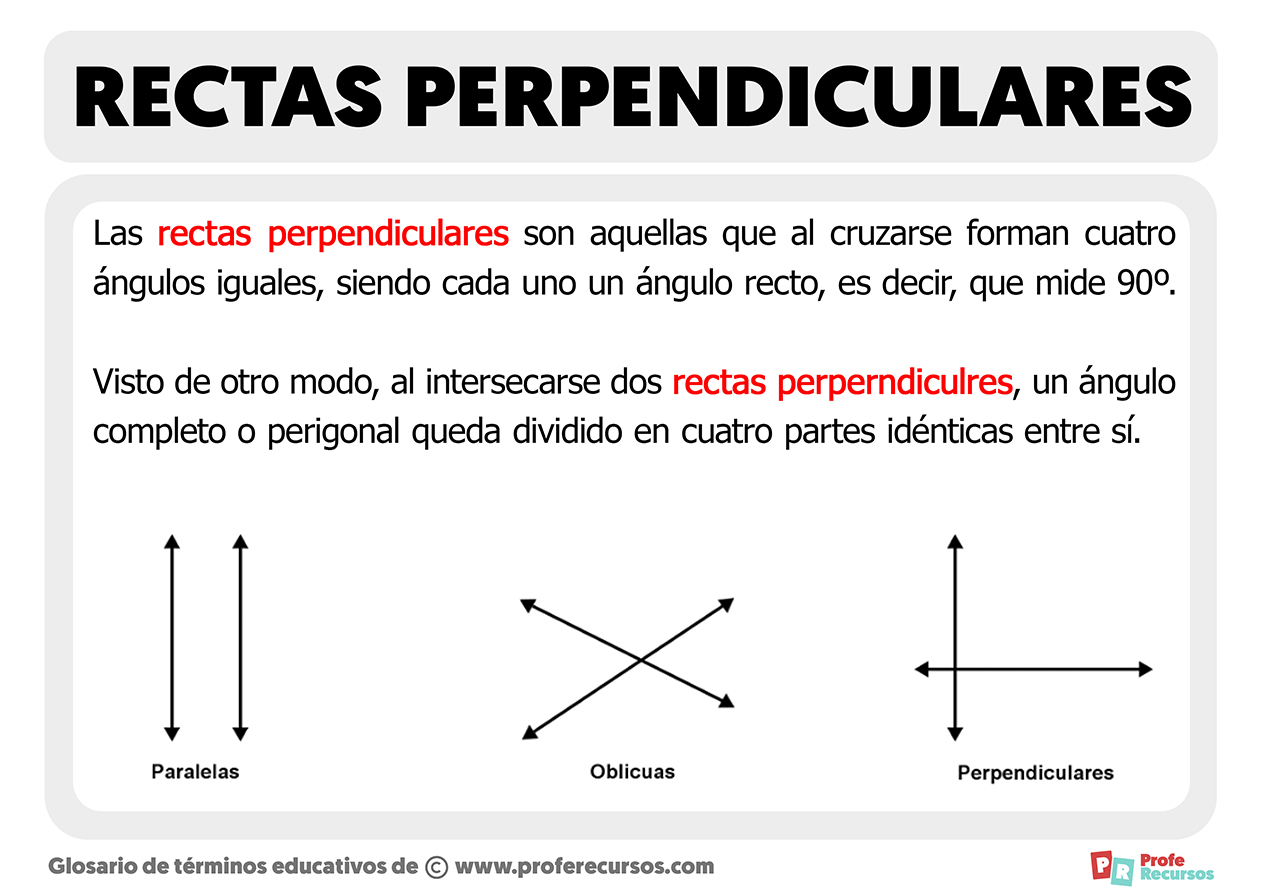
Rectas Perpendiculares Qué Son Y Cómo Funcionan Las rectas perpendiculares. en esta ocasión, te traemos una nueva ficha con el concepto y la representación gráfica de lo que son las rectas perpendiculares. decimos que dos rectas son perpendiculares cuando, al cruzarse, forman cuatro ángulos idénticos. cada uno de estos ángulo que se forman son ángulos rectos., ángulos cuya amplitud. Uso de herramientas de geometría. 4 ejemplos matemáticos de rectas perpendiculares. 4.1 ejemplo 1: cálculo de pendientes. 4.2 ejemplo 2: medición de Ángulos. 5 aplicaciones de las rectas perpendiculares en la vida real. 6 errores comunes al trabajar con rectas perpendiculares. Fórmula. para que dos rectas sean perpendiculares entre sí, además de cumplir la condición de formar un ángulo recto al intersectarse, matemáticamente se debe cumplir la condición: el producto de las pendientes de las rectas sea igual a ( 1). si este principio se da, entonces las rectas son perpendiculares. publicidad, continua debajo. Las siguientes son las propiedades de las líneas perpendiculares: las líneas perpendiculares siempre se intersecan la una con la otra. el ángulo formado entre dos líneas perpendiculares siempre es de 90°. las pendientes de las líneas perpendiculares son recíprocas y negativas la una de la otra. si es que una línea es perpendicular a una.

Perpendicularidad En Sistema Diédrico 10endibujo Fórmula. para que dos rectas sean perpendiculares entre sí, además de cumplir la condición de formar un ángulo recto al intersectarse, matemáticamente se debe cumplir la condición: el producto de las pendientes de las rectas sea igual a ( 1). si este principio se da, entonces las rectas son perpendiculares. publicidad, continua debajo. Las siguientes son las propiedades de las líneas perpendiculares: las líneas perpendiculares siempre se intersecan la una con la otra. el ángulo formado entre dos líneas perpendiculares siempre es de 90°. las pendientes de las líneas perpendiculares son recíprocas y negativas la una de la otra. si es que una línea es perpendicular a una. Ejemplos cotidianos de rectas perpendiculares: las paredes de una habitación: imagina las paredes de una habitación rectangular. las paredes opuestas son perpendiculares entre sí, formando ángulos rectos en las esquinas. las líneas de una cuadrícula: en una hoja cuadriculada, las líneas horizontales y verticales son perpendiculares entre. Solución paso a paso. recordemos que las rectas perpendiculares entre sí que forman un ángulo de 90 grados. en cada una de las respuestas dibujaremos la letra t en el punto de intersección de las líneas. examinemos la figura a: notamos que las rectas no forman un ángulo recto, y por tanto no son perpendiculares.

Comments are closed.