Vector Unitario En El Espacio R3 Ejemplo 1

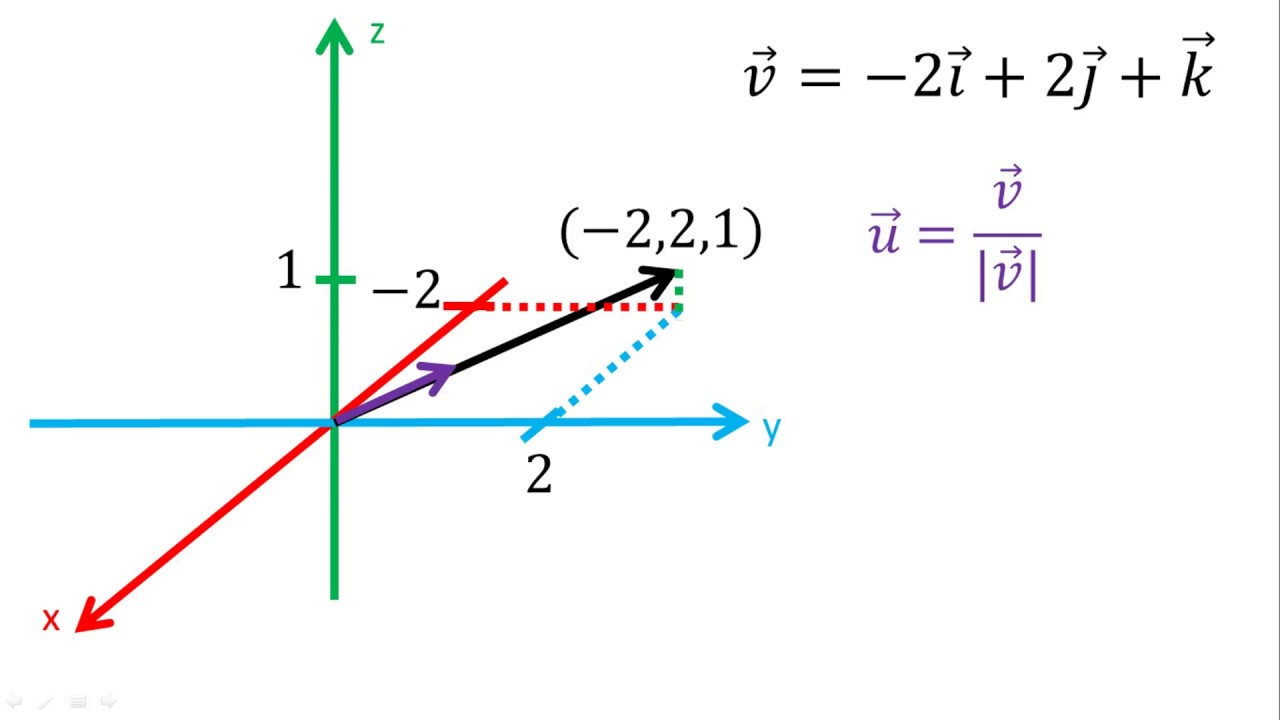
Vector Unitario En El Espacio R3 Ejemplo 1 Youtube En este video se calculará un vector unitario con la misma dirección de un vector con coordenadas (x,y,z). Para ubicar un punto en \ ( {\mathbb {r}^3}\) usaremos como sistema de referencia una terna de ejes perpendiculares entre sí: los cuales se cortan en el punto o (origen de coordenadas). en el siguiente esquema se ven los tres planos que quedan determinados: estos planos se conocen como planos coordenados. el nombre del plano \ (xy\) viene de.

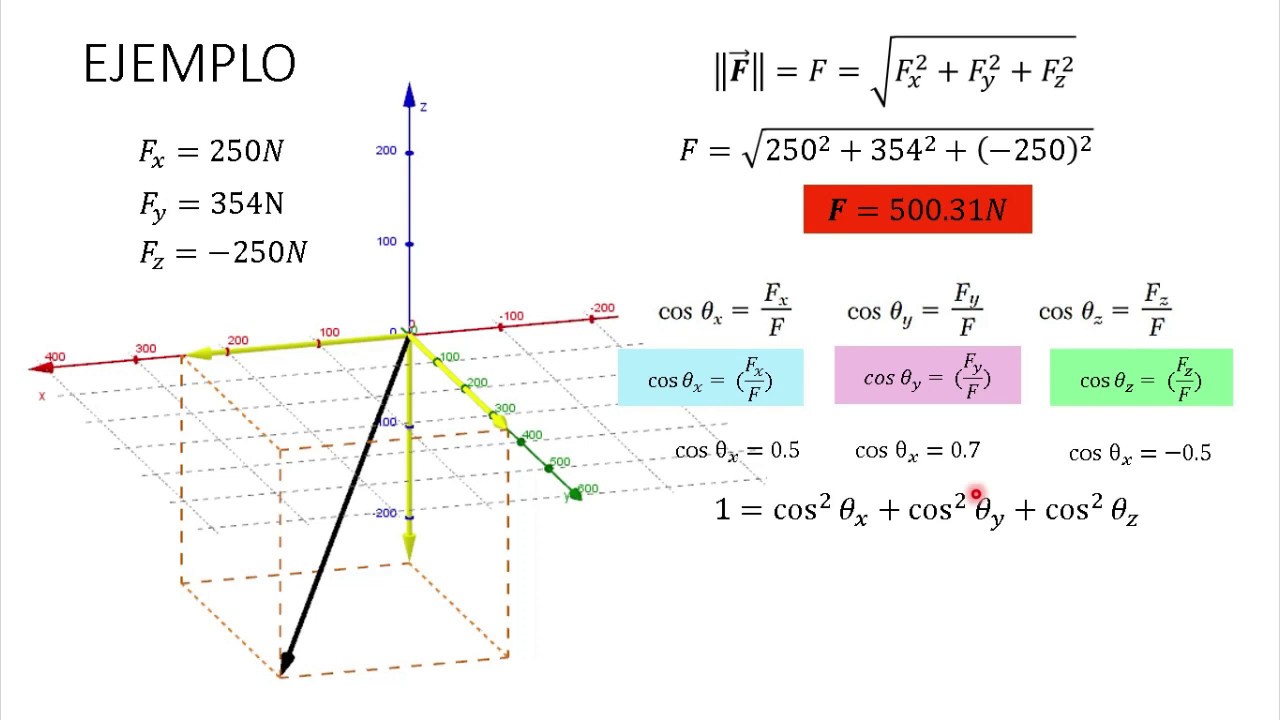
Vectores Unitarios En R3 Youtube Un vector unitario es un vector con una magnitud (longitud) de 1, que apunta en la misma dirección que el vector original. entonces, podemos seguir dos pasos simples para encontrar el vector unitario: paso 1: calcula la magnitud (longitud) del vector original: para un vector \vec {v} = \langle x, y, z\rangle v = x,y,z , la magnitud está dada por:. La ecuación estándar de una esfera con centro (a, b, c) y radio r es (x − a)2 (y − b)2 (z − c)2 = r2. en tres dimensiones, como en dos, los vectores se expresan comúnmente en forma de componentes ⇀ v = x, y, z , o en términos de los vectores unitarios estándar, ⇀ v = xˆi yˆj z ˆk. El producto vectorial en r³, también conocido como producto cruz, se define como una operación entre dos vectores que resulta en un tercer vector que es perpendicular a los dos vectores originales. se representa matemáticamente como: «producto vectorial de a y b»: ( mathbf {c} = mathbf {a} times mathbf {b} ) el resultado ( mathbf {c} ) es. Representaremos cada vector \(\vec{u}\) del espacio real \(\mathbb{r}^3\) como una flecha de una determinada longitud (módulo), que parte de un punto y apunta a otro punto. ejemplo: el vector une a los puntos \(a=(1,1,1)\) y \(b=(2,2, 2)\), con el sentido del punto \(a\) al punto \(b\).

Vector Unitario En El Espacio R3 Ejemplo 2 Youtube El producto vectorial en r³, también conocido como producto cruz, se define como una operación entre dos vectores que resulta en un tercer vector que es perpendicular a los dos vectores originales. se representa matemáticamente como: «producto vectorial de a y b»: ( mathbf {c} = mathbf {a} times mathbf {b} ) el resultado ( mathbf {c} ) es. Representaremos cada vector \(\vec{u}\) del espacio real \(\mathbb{r}^3\) como una flecha de una determinada longitud (módulo), que parte de un punto y apunta a otro punto. ejemplo: el vector une a los puntos \(a=(1,1,1)\) y \(b=(2,2, 2)\), con el sentido del punto \(a\) al punto \(b\). En este video se verá cómo trazar un vector en el espacio tridimensional r3, así como el cálculo de su magnitud. Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. la interpretación geométrica de la suma de vectores, por ejemplo, es la misma en el espacio bidimensional y tridimensional (figura 10.2 18).

Vectores Unitarios En este video se verá cómo trazar un vector en el espacio tridimensional r3, así como el cálculo de su magnitud. Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. la interpretación geométrica de la suma de vectores, por ejemplo, es la misma en el espacio bidimensional y tridimensional (figura 10.2 18).