Vector Unitario En El Espacio Tridimensional R3

Vector Unitario En El Espacio R3 Ejemplo 2 Youtube Para ubicar un punto en \ ( {\mathbb {r}^3}\) usaremos como sistema de referencia una terna de ejes perpendiculares entre sí: los cuales se cortan en el punto o (origen de coordenadas). en el siguiente esquema se ven los tres planos que quedan determinados: estos planos se conocen como planos coordenados. el nombre del plano \ (xy\) viene de. Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. la interpretación geométrica de la adición vectorial, por ejemplo, es la misma tanto en el espacio bidimensional como en el tridimensional (figura \(\pageindex{19}\)).

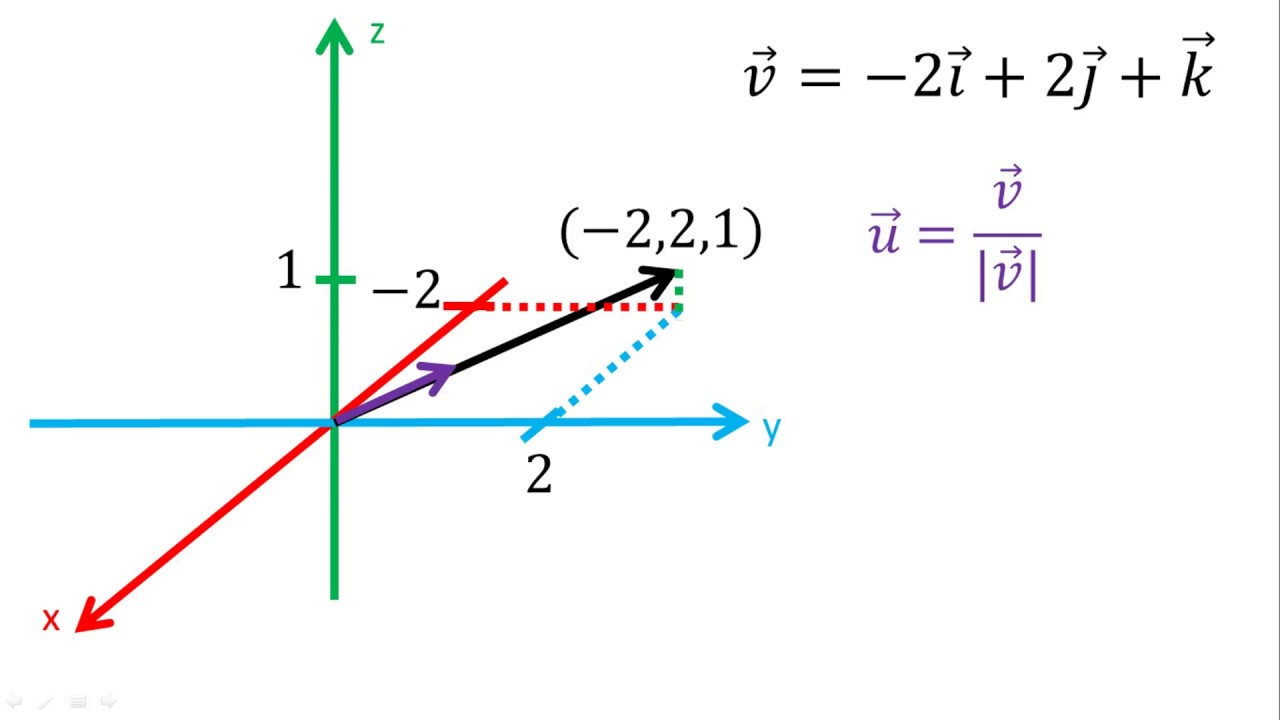
Vector Unitario En El Espacio R3 Ejemplo 1 Youtube En este video se muestra la manera de calcular un vector unitario en el espacio tridimensional x,y,z. 2.2.1 describir matemáticamente el espacio tridimensional. 2.2.2 localizar puntos en el espacio mediante coordenadas. 2.2.3 escribir la fórmula de la distancia en tres dimensiones. 2.2.4 escribir las ecuaciones de planos y esferas simples. 2.2.5 realizar operaciones vectoriales en ℝ 3. ℝ 3. El producto vectorial en r³, también conocido como producto cruz, se define como una operación entre dos vectores que resulta en un tercer vector que es perpendicular a los dos vectores originales. se representa matemáticamente como: «producto vectorial de a y b»: ( mathbf {c} = mathbf {a} times mathbf {b} ) el resultado ( mathbf {c} ) es. Estructura del espacio vectorial real r^3, definición de vector, vector fijo, vector libre, vector que une dos puntos, módulo de un vector. geometría tridimensional para bachillerato. teoría, ejemplos y problemas resueltos, ejemplos. espacio afín real tridimensional. con representaciones gráficas.

Análisis Vectorial Todo Sobre Vectores En Física El producto vectorial en r³, también conocido como producto cruz, se define como una operación entre dos vectores que resulta en un tercer vector que es perpendicular a los dos vectores originales. se representa matemáticamente como: «producto vectorial de a y b»: ( mathbf {c} = mathbf {a} times mathbf {b} ) el resultado ( mathbf {c} ) es. Estructura del espacio vectorial real r^3, definición de vector, vector fijo, vector libre, vector que une dos puntos, módulo de un vector. geometría tridimensional para bachillerato. teoría, ejemplos y problemas resueltos, ejemplos. espacio afín real tridimensional. con representaciones gráficas. En este video se calculará un vector unitario con la misma dirección de un vector con coordenadas (x,y,z). El vector normal unitario y el vector binormal forman un plano que es perpendicular a la curva en cualquier punto de la misma, llamado plano normal. además, estos tres vectores forman un marco de referencia en el espacio tridimensional llamado marco de referencia frenet (también llamado marco tnb ) ( figura 3.7 ).

Vectores Unitarios En este video se calculará un vector unitario con la misma dirección de un vector con coordenadas (x,y,z). El vector normal unitario y el vector binormal forman un plano que es perpendicular a la curva en cualquier punto de la misma, llamado plano normal. además, estos tres vectores forman un marco de referencia en el espacio tridimensional llamado marco de referencia frenet (también llamado marco tnb ) ( figura 3.7 ).