Vectores En El Espacio Que Son Aplicaciones Notacion Ejercicios
Vectores En El Espacio Qué Son Aplicaciones Notación Ejercicios Por fanny zapata. licenciada en física, con mención en física experimental. Última edición el 29 de noviembre de 2023. un vector en el espacio es todo vector representado mediante un sistema de coordenadas dado por x, y y z. casi siempre el plano xy es el plano de la superficie horizontal y el eje z representa la altura (o profundidad). Los vectores en el plano se visualizan en un sistema de coordenadas, permitiendo la representación gráfica de operaciones como la suma y la resta de vectores. por ejemplo, si tenemos dos vectores v1 = (x1, y1) y v2 = (x2, y2), su suma sería v1 v2 = (x1 x2, y1 y2). esto permite a los matemáticos y científicos representar diversos.
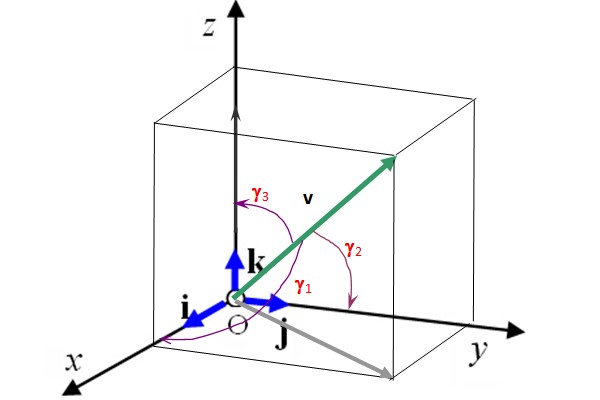
Vectores En El Espacio Qué Son Aplicaciones Notación Ejercicios La ecuación estándar de una esfera con centro (a, b, c) y radio r es (x − a)2 (y − b)2 (z − c)2 = r2. en tres dimensiones, como en dos, los vectores se expresan comúnmente en forma de componentes ⇀ v = x, y, z , o en términos de los vectores unitarios estándar, ⇀ v = xˆi yˆj z ˆk. 2.1. vectores fijos y vectores libres (en el plano y en el espacio) el vector que tiene por origen el punto a y por extremo el punto b, se llama vector fijo ab. − módulo del vector es la longitud del segmento ab. se denota ab. − dirección de es la de la recta que contiene a a y a b. − sentido de es el que indica el traslado de a a b. V 1 = v ‖ v ‖ = 1 ‖ v ‖ v. y, de forma totalmente análoga a los vectores en el plano, definimos las operaciones con vectores en el espacio: definition (suma de vectores y multiplicación por un escalar en 3d) sean u = (u 1, u 2, u 3) y v = (v 1, v 2, v 3) vectores y sea c ∈ r un escalar. el múltiplo escalar de c y u es el vector c u. En ejercicios 27 32,vecv se dan vectores→u y. escribe →u como la suma de dos vectores, uno de los cuales es paralelo→v y uno de los cuales es perpendicular a→v. nota: estos son los mismos pares de vectores que se encuentran en los ejercicios 21 26. 27. →u = 1, 2 , →v = − 1, 3 . 28. →u = 5, 5 , →v = 1, 3 .

Vectores En El Espacio Qué Son Aplicaciones Notación Ejercicios V 1 = v ‖ v ‖ = 1 ‖ v ‖ v. y, de forma totalmente análoga a los vectores en el plano, definimos las operaciones con vectores en el espacio: definition (suma de vectores y multiplicación por un escalar en 3d) sean u = (u 1, u 2, u 3) y v = (v 1, v 2, v 3) vectores y sea c ∈ r un escalar. el múltiplo escalar de c y u es el vector c u. En ejercicios 27 32,vecv se dan vectores→u y. escribe →u como la suma de dos vectores, uno de los cuales es paralelo→v y uno de los cuales es perpendicular a→v. nota: estos son los mismos pares de vectores que se encuentran en los ejercicios 21 26. 27. →u = 1, 2 , →v = − 1, 3 . 28. →u = 5, 5 , →v = 1, 3 . 1 para que los vectores sean ortogonales su producto escalar tiene que ser igual a cero. luego los vectores son ortogonales si . 2 para qué dos vectores sean paralelos, sus componentes tienen que ser proporcionales. se obtiene el sistema. el cual no tiene solución, por tanto los vectores no son paralelos para cualquier valor de. Coordenadas en el espacio. los vectores del espacio se representan en un sistema de corrdenadas tridimnensional. el sistema se consigue trazando un eje z perpendicular en el origen de coordenadas a los ejes x e y. un punto p viene determinado por p (x, y, z).

Vectores En El Espacio Producto Punto Interpretacion Geometrica Aplicaciones Ejercicios 1 para que los vectores sean ortogonales su producto escalar tiene que ser igual a cero. luego los vectores son ortogonales si . 2 para qué dos vectores sean paralelos, sus componentes tienen que ser proporcionales. se obtiene el sistema. el cual no tiene solución, por tanto los vectores no son paralelos para cualquier valor de. Coordenadas en el espacio. los vectores del espacio se representan en un sistema de corrdenadas tridimnensional. el sistema se consigue trazando un eje z perpendicular en el origen de coordenadas a los ejes x e y. un punto p viene determinado por p (x, y, z).

Comments are closed.